The paper Neural Posterior Estimation of Neutron Star Equations of State, by Valéria Carvalho, Márcio Ferreira, Michał Bejger (from Copernicus Astronomical Center in Warsaw and INFN in Ferrara), Constança Providência,introduces a machine learning, simulation-based inference framework for inferring the equation of state (EoS) of neutron star matter from astrophysical data using neural posterior estimation (NPE). In this approach, a neural network learns to approximate the full probability distribution (the posterior) of possible EoS models given observed quantities, such as stellar masses, radii, or tidal deformabilities. Unlike traditional methods that rely on explicit likelihood functions or fixed EoS parametrizations, the network is trained on simulated data and learns the mapping in a likelihood-free manner. To keep the results physically meaningful, the training incorporates consistency constraints that enforce causality (the speed of sound never exceeding the speed of light) and thermodynamic stability (pressure increasing with density).
Beyond reproducing pressures, sound speeds, and other thermodynamic variables with calibrated uncertainties, the method exhibits a notable sensitivity to the maximum central density of neutron stars: its predictive uncertainty correlates strongly with this quantity, even though the model is not explicitly trained on it. This suggests that the network is picking up on physical structure intrinsic to the data.
Presented methods are relevant for multi-messenger astronomy. Gravitational-wave observations from the LIGO-Virgo-KAGRA (LVK) collaboration constrain tidal deformabilities during binary mergers, while X-ray timing data from NICER provide radius and mass estimates for individual pulsars. The proposed method can incorporate both types of data, with or without tidal deformabilities, and return calibrated probability distributions over the EoS. This means it offers a unified way to combine different observational channels under minimal assumptions, potentially sharpening constraints on the properties of ultra-dense matter.
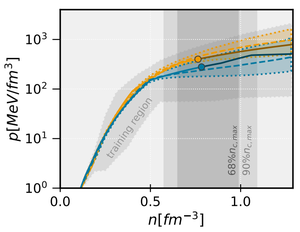
Figure caption:Examples of pressure p as a function of density n reconstruction for selected equations of state relations.
Text and illustration by Michał Bejger.






