W artykule Neural Posterior Estimation of Neutron Star Equations of State, autorstwa Valéria Carvalho, Márcio Ferreira, Michał Bejger (z Centrum Astronomicznego im. M. Kopernika w Warszawie i INFN w Ferrarze), Constança Providência, przedstawiono oparty na uczeniu maszynowym i symulacjach system wnioskowania, umożliwiający ustalenie równania stanu (EoS) materii gwiazd neutronowych na podstawie danych astrofizycznych, z wykorzystaniem neuronowej estymacji a posteriori (NPE). W tym podejściu sieć neuronowa uczy się przybliżać pełny rozkład prawdopodobieństwa (a posteriori) możliwych modeli EoS, uwzględniając obserwowane wielkości, takie jak masy gwiazd, promienie lub deformacje pływowe. W przeciwieństwie do tradycyjnych metod, które opierają się na jawnych funkcjach prawdopodobieństwa lub stałej parametryzacji EoS, sieć jest trenowana na danych symulowanych i uczy się mapowania w sposób niezależny od prawdopodobieństwa. Aby wyniki były fizycznie miarodajne, trening uwzględnia ograniczenia spójności, które wymuszają przyczynowość (prędkość dźwięku nigdy nie przekracza prędkości światła) i stabilność termodynamiczną (ciśnienie rośnie wraz z gęstością).
Poza odtwarzaniem ciśnień, prędkości dźwięku i innych zmiennych termodynamicznych ze skalibrowanymi niepewnościami, metoda ta wykazuje znaczną czułość na maksymalną gęstość centralną gwiazd neutronowych: jej niepewność przewidywania silnie koreluje z tą wartością, mimo że model nie został na niej bezpośrednio wytrenowany. Sugeruje to, że sieć wychwytuje strukturę fizyczną właściwą danym.
Zaprezentowane metody są istotne dla astronomii wieloaspektowej. Obserwacje fal grawitacyjnych z projektu LIGO-Virgo-KAGRA (LVK) ograniczają deformacje pływowe podczas łączenia się układów podwójnych, podczas gdy dane czasowe promieniowania rentgenowskiego z NICER pozwalają oszacować promień i masę poszczególnych pulsarów. Proponowana metoda może uwzględniać oba rodzaje danych, z deformacjami pływowymi lub bez, i zwracać skalibrowane rozkłady prawdopodobieństwa dla stanu równowagi. Oznacza to, że oferuje ona ujednolicony sposób łączenia różnych kanałów obserwacyjnych przy minimalnych założeniach, potencjalnie zaostrzając ograniczenia dotyczące właściwości materii ultragęstej.
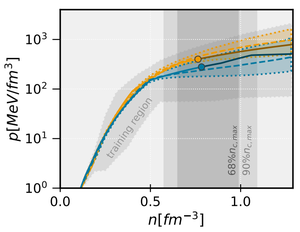
Rysunek: Przykłady rekonstrukcji ciśnienia p w funkcji gęstości n dla wybranych równań stanu.
Tekst i ilustracja: Michał Bejger.






