In a paper published recently in Physical Review, "Can We Make Sense of Dissipation without Causality?", Lorenzo Gavassino, studies the problem of stability in relativity theory. In the years 2018-2022 author was a Ph.D. student at the Copernicus Astronomical Center in Warsaw under supervision of Brynmor Haskel. He received his degree in 2022. Most of the presented results Lorenzo obtained during his stay at in Warsaw. Currently he is a pot-doc at Vanderbilt University in Nashville, TN, United States.
Many dissipative processes in physics are currently modeled using equations that allow for faster-than-light communication. The most cited example is the heat equation, which permits energy transport at infinite speed. Equations of this kind are very popular also in relativistic settings (especially in relativistic astrophysics) and are employed in theoretical models and numerical simulations. Should we be worried? In this work, we find that the answer is probably yes.
We show that, when a system of partial differential equations violates causality, different observers disagree on whether the system tends to evolve toward thermodynamic equilibrium or away from it. In other words, acausal dissipative systems that are stable in one reference frame always end up being unstable in another. In causal theories, on the other hand, the equilibrium state is either stable or unstable in all reference frames at the same time.
One implication of this paper is that in relativity, we can never rely on acausal dissipative field equations, even when our intuition may suggest that faster-than-light signals may be “negligible.” They are not. There is always a reference frame in which causality violations produce infinitely fast instabilities that destroy the system in a fraction of a nanosecond. However, there is also some good news: If causality holds, stability (or instability) is a Lorentz-invariant property of the field equations. Hence, there is no need to assess the stability of a theory in reference frames in which the background is moving. One can always work in the rest frame of the medium.
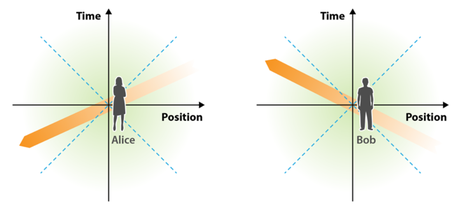
Figure caption:
In Alice’s reference frame (left), a perturbation to a fluid moves superluminally from left to right. Its intensity (orange) decreases with time as a result of dissipation. For Bob (right), who is in motion relative to Alice, the perturbation moves from right to left, and its intensity grows with time. For both Bob and Alice, the superluminal perturbation falls outside of the light cone (blue dashed lines) and violates causality. This simple point-of-view analysis leads to a stability criterion for any relativistic-fluid-dynamical theory: a theory that is stable and causal in one reference frame is stable in all reference frames.






